Question

A manufacturer reports that the mean lifetime of its lithium batteries is 1100 hours, but there are customer complaints that the battery life is lower. A consumer advocate group selects 25 of these batteries at random and finds the mean lifetime to be 1080 hours with a standard deviation of 80 hours. The sample data are approximately symmetric and unimodal with no outliers. Check conditions, show how the test statistic is calculated. Test using a 10% significance level. State your conclusion in the context of the problem.

Answer 1

The p-value of the test is 0.1117 > 0.1, which means that there is not significant evidence at the 10% significance level that the battery life is lower than 1100 hours.

Explanation:

A manufacturer reports that the mean lifetime of its lithium batteries is 1100 hours, but there are customer complaints that the battery life is lower.

At the null hypothesis, we test that the mean lifetime of the battery is of 1100 hours, that is:

`H_0: \mu = 1100`

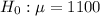
At the alternate, we test that is is lower, that is:

`H_a: \mu < 1100`

The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

1100 is tested at the null hypothesis:

This means that
`\mu = 1100`

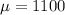
A consumer advocate group selects 25 of these batteries at random and finds the mean lifetime to be 1080 hours with a standard deviation of 80 hours.

This means that
`n = 25, X = 1080, s = 80`

Test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (1080 - 1100)/((80)/(√(25)))`

`t = -1.25`

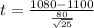
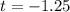
P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean below 1080, which is found using a left-tailed test for t = -1.25, with 25 - 1 = 24 degrees of freedom.

With the help of a calculator, this p-value is of 0.1117

The p-value of the test is 0.1117 > 0.1, which means that there is not significant evidence at the 10% significance level that the battery life is lower than 1100 hours.