Question

A landscaper is designing a flower garden in the shape of a trapezoid. She wants the shorter base to be 3 yards

greater than the height and the longer base to be 7 yards greater than the height. She wants the area to be 155
square yards. The situation is modeled by the equation h2 + 5h 155. Use the Quadratic Formula to find the
height that will give the desired area. Round to the nearest hundredth of a yard.
320 yards
c. 20.4 yards
b. 10.2 yards
d. 12.7 yards
a.

Answer 1

9514 1404 393

Answer:

b. 10.2 yards

Explanation:

The quadratic formula tells you the solutions to ...

ax² +bx +c = 0

are given by ...

`x=(-b\pm√(b^2-4ac))/(2a)`

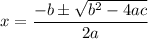
Here, the quadratic equation we have is ...

h² +5h -155 = 0

So the solutions given by the quadratic formula are ...

`h=(-5\pm√(5^2-4(1)(-155)))/(2(1))=(-5\pm√(645))/(2)=\{-15.2,10.2\}`

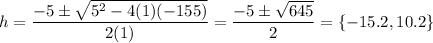
The negative solution is not applicable in this situation, so the height that gives the desired area is 10.2 yards.