Question

Find the length DE. Round your answer to the nearest tenth of a meter

Answer 1

13.8

Explanation:

We can use trigonometry to find the length of DE

Remember these are the trigonometric ratios

Sin = Opposite over Hypotenuse

Cos = Adjacent over Hypotenuse

Tan = Opposite over Adjacent

For ∠FDE we are given its opposite side length ( FE ) and need to find its adjacent angle ( DE )

When working with opposite and adjacent we use the trig ratio tangent

That being said we want to create an equation to solve for (DE) ( Recall that tan = opposite over adjacent. ) ( let DE = x )

so
`tan(51)=(17)/(x)`

now we solve for x

Step 1 multiply each side by x

tan(51) * x = x tan (51)

`(17)/(x) *x=17`

now we have x tan (51) = 17

step 2 divide each side by tan (51)

`(xtan(51))/(tan(51))=x\\(17)/(tan(51))`

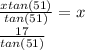
we now have

`x =(17)/(tan(51)) \\`

`tan(51)=1.234897157\\(17)/(1.234897157) =13.76632856`

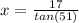
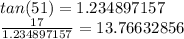
we're left with x = 13.76632856

Finally we round to the nearest tenth and get that the answer 13.8