The length of AB is approximately 19.13 units (rounded to the nearest tenth).
To find the length of AB, we can use the Power of a Point Theorem. This theorem states that for any point P outside a circle, the product of the lengths of the two segments that a secant line (or a chord extended) divides the circle into is equal. Mathematically, if
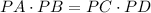 , then point P lies on the circle.
, then point P lies on the circle.
In this case, let point P be the extension of line AB to line AC. The segments are PA = AB and PB = BC. The other segments are PC = PD = AC.
So, we have:
![\[AB \cdot BC = AC \cdot AC\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/m7g46709n3cetzrfls4o182yacbj009ejr.png)
Substitute the given values:
![\[AB \cdot 15 = AC \cdot AC\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/d6s4s5314vbn1bvmfac377qnr1n2qz0g3m.png)
Given that AD = 8, we can find AC using the Pythagorean Theorem:
![\[AC = √(AD^2 + CD^2) = √(8^2 + 15^2) = √(64 + 225) = √(289) = 17\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4awh4pzrw3l1eap0vhr4tnd5dglplkqyb4.png)
Now, substitute this value back into the equation:
![\[AB \cdot 15 = 17 \cdot 17\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ut4ne4mll2lgp1uxx4cwtp0vmn5hc77lcx.png)
![\[AB = (17 \cdot 17)/(15) \approx 19.13\]](https://img.qammunity.org/2022/formulas/mathematics/high-school/u1txk4yoqtzl3tevil2k72grbrirzwhvgj.png)
Therefore, the length of AB is approximately 19.13 units (rounded to the nearest tenth).