Solution :
As we can see from the following question that :
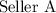 charges
charges
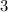 for their house,
for their house,
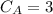
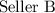 charges
charges
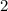 for their house,
for their house,
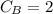
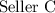 charges
charges
 for their house,
for their house,

Now depending on the valuation that each buyer have on these three houses, they derive utility from it :
Buyer I
Valuation for house A,
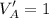
Valuation for house B,

Valuation for house C,
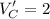
Utility that buyer I derives from :
House A,
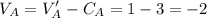
House B,
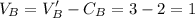
House C,
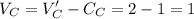
As we can see from buying house B and C, buyer I has positively utility, so the buyer will be interested to buy house B and C. As the utility derived from both the houses is same, he will be indifferent.
Buyer II
Valuation for house A,
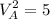
Valuation for house B,
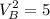
Valuation for house C,

Utility that buyer II derives from :
House A,
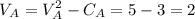
House B,

House C,
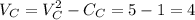
Buyer II drives positive utility from all the three houses, so he will be interested to buy any of them but will be inclined towards house C, as it gives the buyer more utility.
Buyer III
Valuation for house A,
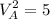
Valuation for house B,
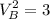
Valuation for house C,
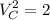
Utility that buyer III derives from :
House A,
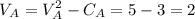
House B,
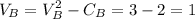
House C,
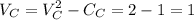
The buyer III derives positive utility from all the three houses but will be more inclined to buy house A as it gives the buyer higher utility as compared to the other houses.