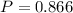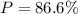Question

Cast Iron Company, on each nondelinquent sale, receives revenues with a present value of $1,230 and incurs costs with a value of $1,065. Cast Iron has been asked to extend credit to a new customer. You can find little information on the firm, and you believe that the probability of payment is no better than 0.77. But if the payment is made, the probability that the customer will pay for the second order is 0.94. It costs $15.25 to determine whether a customer has been a prompt or slow payer in the past.

Calculate the minimum probability at which credit can be extended. (round answer 2 decimal places)

Answer 1

`P=0.866`

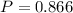
Explanation:

From the question we are told that:

Present value of iron
`x_v=\$1230`

Present cost of iron
`x_c=\$1065`

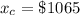
Probability of payment
`P_p=0.77`

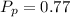
Probability that the customer will pay for the second order
`P_s=0.94`

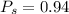
Cost of knowing customer status
`x_k=\$15.25`

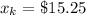
Generally the equation for Expected probability
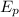`E_p` is mathematically given by

`E_p=(probability*(revenue-cost)-(1-probability)*present\ value\ of\ cost)`

`E_p=(P*(x_v-x_c)-(1-P)*X_c)`

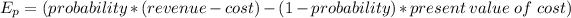
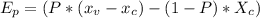
Where

`E_p=0`

`P=minimum\ probability\ at\ which\ credit\ can\ be\ extended`

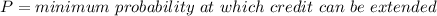
Therefore

`0=(P*(1230-1065)-(1-P)*1065)`

`165P-1065+1065P=0`

`P=(1065)/(1230)`

`P=0.866`

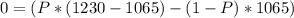
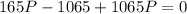
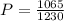
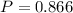
Therefore the minimum probability at which credit can be extended is given as

`P=0.866`

`P=86.6\%`