Question

vTo estimate the parameter stated in question 2, the following was done. A simple random sample of 22 students who attended a review session was selected, and the mean grade on test 7 for this sample of 22 students was 85 with a standard deviation of 9.8. An independent simple random sample of 47 students who did not attend a review session was selected, and the mean grade on test 7 was 77 with a standard deviation of 10.6. If appropriate, use this information to calculate and interpret a 90% confidence interval for the difference in the mean grade on test 7 for all students who attended a review session and for all students who did not attend a review session.

Answer 1

The 90% confidence interval for the difference in the mean grade on test 7 for all students who attended a review session and for all students who did not attend a review session is (3.7, 12.3).

Explanation:

Before building the confidence interval, we need to understand the central limit theorem and subtraction between normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

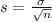For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
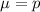`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

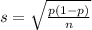
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

A simple random sample of 22 students who attended a review session was selected, and the mean grade on test 7 for this sample of 22 students was 85 with a standard deviation of 9.8.

This means that:

`\mu_A = 85, s_A = (9.8)/(√(22)) = 2.09`

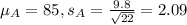
An independent simple random sample of 47 students who did not attend a review session was selected, and the mean grade on test 7 was 77 with a standard deviation of 10.6.

This means that:

`\mu_N = 77, s_N = (10.6)/(√(47)) = 1.55`

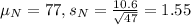
Distribution of the difference in the mean grade on test 7 for all students who attended a review session and for all students who did not attend a review session.

Mean:

`\mu = \mu_A - \mu_N = 85 - 77 = 8`

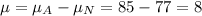
Standard deviation:

`s = √(s_A^2 + s_B^2) = √(2.09^2 + 1.55^2) = 2.6`

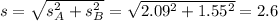
Confidence interval:

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1 - 0.9)/(2) = 0.05`

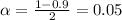
Now, we have to find z in the Ztable as such z has a pvalue of
`1 - \alpha`.

That is z with a pvalue of
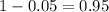`1 - 0.05 = 0.95`, so Z = 1.645.

Now, find the margin of error M as such

`M = zs`

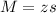
So

`M = 1.645*2.6 = 4.3`

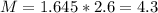
The lower end of the interval is the sample mean subtracted by M. So it is 8 - 4.3 = 3.7

The upper end of the interval is the sample mean added to M. So it is 8 + 4.3 = 12.3

The 90% confidence interval for the difference in the mean grade on test 7 for all students who attended a review session and for all students who did not attend a review session is (3.7, 12.3).