Answer:
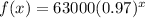
Explanation:
Given
 ---x = 0, in 2012
---x = 0, in 2012
 -- x = 5, in 2017
-- x = 5, in 2017
Required
Select all possible equations
Because there is a reduction in the population, as time increases; the rate must be less than 1.
An exponential function is represented as:
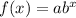
Where
rate > 1 in options (a) and (b) i.e. 1.03
This implies that (a) and (b) cannot be true
For option (c), we have:
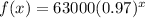
Set x = 0
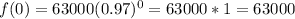
Set x = 5
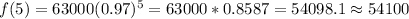
This is true because the calculated values of f(0) and f(5) correspond to the given values
For option (d), we have:
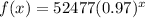
Set x = 0
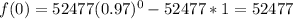
This is false because the calculated value of f(0) does not correspond to the given value
For option (e), we have:
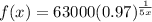
Set x = 0
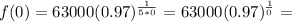 undefined
undefined
This is false because the f(x) is not undefined at x = 0
For option (f), we have:
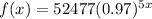
Set x = 0

This is false because the calculated value of f(0) does not correspond to the given value
From the computations above, only (c)
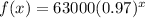 is true
is true