Question

Suppose that you make a series RC circuit with a capacitor and a known resistor that has a 5% tolerance: R= 5.20 ± 0.26kΩ. You plan is to measure the time constant of the circuit in order to determine the value of the capacitor. You do ten trials of your experiment and measure the time constant each time, and then you calculate the average and standard error of the ten results to determine that τ= 2.150 ± 0.002s.

Which of the following is the best estimate of the uncertainty on your determination of the value of your capacitor?
a. 1%
b. 0.1%
c. 5%

Answer 1

correct answer is C

Step-by-step explanation:

The time constant of an RC circuit is

τ = RC

so to find the capacitance

C = τ/ R

C = 2.150 / 5.20 10³

C = 4.13 10⁻⁴ F

to find the error we use the worst case

ΔC = |
`|(dC)/(d \tau )| \ \Delta \tau + | (dC)/(dR) | \ \Delta R`

the absolute value guarantees that we find the worst case, we evaluate the derivatives

ΔC = 1 /R Δτ + τ/R² ΔR

the absolute values ​​of the errors are

Δτ = 0.002 s

ΔR = 0.3 kΩ

we substitute

ΔC = 0.002 /5.20 10³ + 2.150/(5.20 10³)² 0.3 10³

ΔC = 3.8 10⁻⁷ + 1.74 10⁻⁵

ΔC = 1.77 10⁻⁵ F

the uncertainty or error must be expressed with a significant figure

ΔC = 2 10⁻⁵ F

the percentage error is

Er% =
`(\Delta C)/(C) \ 100`

Er% =
`(2 \ 10^(-5) )/( 4.13 \ 10^(-4) ) \ 100`

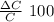
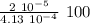
Er% = 4.8%

the correct answer is C