Here , the given function to us is
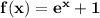 which is clearly an exponential function , so it's inverse will be a logarithmic function . So , now let's solve for it's inverse
which is clearly an exponential function , so it's inverse will be a logarithmic function . So , now let's solve for it's inverse
We have ;
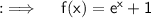
Now , let y = f(x) . So :
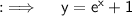
Now , solve for x
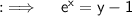
Take natural log on both sides :
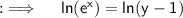
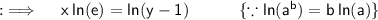
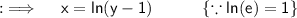
Now , replace x by
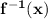 and y by x
and y by x
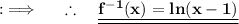
Now , we got the inverse of f(x) which is a logarithmic function with domain
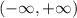 and Range
and Range
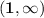 .So , the domain is the set of all real numbers and range being y > 1
.So , the domain is the set of all real numbers and range being y > 1
Hence , The required answers are a logarithmic, all real numbers and y > 1