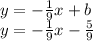Question

Write an equation in slope-intercept form for the following line:

(-14,1) and (13,-2)

Answer 1

`\large \boxed{y = - (1)/(9) x - (5)/(9) }`

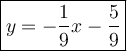
Explanation:

In order to find an equation of a line with two given ordered pairs. We have to find a slope first which we can do by using the formula below.

`\large \boxed{m = (y_2 - y_1)/(x_2 - x_1) }`

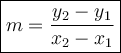
m-term is defined as slope in y = mx+b form which is slope-intercept form.

Now we substitute these ordered pairs (x, y) in the formula.

`\large{m = (1 - ( - 2))/( -14 - 13) } \\ \large{m = (1 + 2)/( - 27) } \\ \large{m = (3)/( - 27) = - (1)/(9) }`

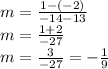
After we calculate for slope, we substitute m-value in slope-intercept form. The slope-intercept form is

`\large \boxed{y = mx + b}`

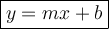
We already know m-value as we substitute it.

`\large{y = - (1)/(9) x + b}`

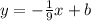
We are not done yet because we need to find the b-term which is our y-intercept. (Note that m-term is slope while b-term is y-intercept)

We can find the y-intercept by substituting either (-14,1) or (13,-2) in the equation. I will be using (13,-2) to substitute in the equation.

`\large{y = - (1)/(9) x + b} \\ \large{ - 2 = - (1)/(9) (13) + b} \\ \large{ - 2 = - (13)/(9) + b} \\ \large{ - 2 + (13)/(9) = b} \\ \large{ - (5)/(9) = b}`

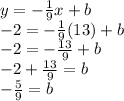
Finally, we know b-value. Then we substitute it in our equation.

`\large{y = - (1)/(9) x + b} \\ \large{y = - (1)/(9) x - (5)/(9) }`