Question

A diver comes off a board with arms straight up and legs straight down, giving her a moment of inertia about her rotation axis of 18kg⋅m2. She then tucks into a small ball, decreasing this moment of inertia to 3.6kg⋅m2. While tucked, she makes two complete revolutions in 1.2s.

Required:
If she hadn't tucked at all, how many revolutions would she have made in the 1.5 s from board to water?

Answer 1

θ₁ = 0.5 revolution

Step-by-step explanation:

We will use the conservation of angular momentum as follows:

`L_1=L_2\\I_1\omega_1=I_2\omega_2`

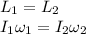
where,

I₁ = initial moment of inertia = 18 kg.m²

I₂ = Final moment of inertia = 3.6 kg.m²

ω₁ = initial angular velocity = ?

ω₂ = Final Angular velocity =
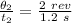`(\theta_2)/(t_2) = (2\ rev)/(1.2\ s)` = 1.67 rev/s

Therefore,

`(18\ kg.m^2)\omega_1 = (3.6\ kg.m^2)(1.67\ rev/s)\\\\\omega_1 = ((3.6\ kg.m^2)(1.67\ rev/s))/((18\ kg.m^2))\\\\\omega_1 = (\theta_1)/(t_1) = 0.333\ rev/s\\\\\theta_1 = (0.333\ rev/s)t_1`

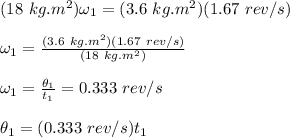
where,

θ₁ = revolutions if she had not tucked at all = ?

t₁ = time = 1.5 s

Therefore,

`\theta_1 = (0.333\ rev/s)(1.5\ s)\\`

θ₁ = 0.5 revolution