Answer:
a) P (0 defective component) = 0.5
P( 1 defective component ) = 0.35
P( 2 defective component ) = 0.15
b) P( 0 ) = 0
p ( 1 ) = 1
p ( 2 ) = 0.33
Explanation:
p( no defective ) = 0.5
p( 1 is defective ) = 0.35
p( 2 is defective ) = 0.15
Given that 2 components are selected at random
a) Given that neither component is defective
Probability of 0 defective component = 0.5
P( 1 defective component ) = 0.35
P( 2 defective component ) = 0.15
b) Given that one of the two tested component is defective
P( 0 defective ) = 0
P( 1 defective ) = P (
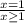 ) = p( x = 1 ) / 1 - P ( x = 0 )
) = p( x = 1 ) / 1 - P ( x = 0 )
= ( 0.5 )^1 ( 0.5 )^0 / 1 - ( 0.5)^0 (0.5)^1
= 0.5 * 1 / 1 - 0.5 = 0.5 / 0.5 = 1
p ( 2 defective ) = p( x = 3 ) / 1 - P ( x = 0 )
= ( 0.5 )^2 ( 0.5 )^0 / 1 - ( 0.5)^0 (0.5)^2
= 0.25 / 0.75 = 0.33