Given:
4, x, y, 108 are the consecutive terms of a G.P.
To find:
The x and y.
Solution:
The nth term of a G.P. is:
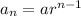
Where, a is the first term and r is the common ratio.
Let us consider 4, x, y, 108 are the first 4 terms of the G.P. Here 4 is the first term of the given G.P.
Suppose r the common ratio, then 4th term of the given G.P. is:
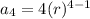
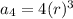
The 4th term of the G.P. is 108.
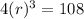
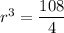
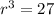

On comparing both sides, we get

The common ratio is 3.
The second term of the given G.P. is:
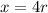

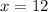
The third term of the given G.P. is:
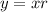
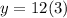
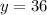
Therefore, the value x is 12 and the value of y is 36.