Two cards are drawn from a standard deck of cards without replacement. Find the probability of drawing a heart and a club in that order

Question

asked Oct 8, 2022 21.4k views

1 Answer

GOVIND DIXIT · Answer 1 · 2022-10-12T14:09:00+0000

Given:

Two cards are drawn from a standard deck of cards without replacement.

To find:

The probability of drawing a heart and a club in that order.

Solution:

We have,

Total number of cards = 52

Number of cards of each suit (Spade, club, diamond, heart) = 13

The probability of drawing a heart card is:

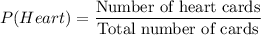
$P(Heart)=\frac{\text{Number of heart cards}}{\text{Total number of cards}}$

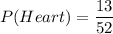
P(Heart)=(13)/(52)

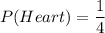
P(Heart)=(1)/(4)

Now, the number of remaining card is 51. So, the probability of drawing a club card is:

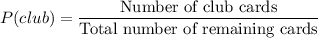
$P(club)=\frac{\text{Number of club cards}}{\text{Total number of remaining cards}}$

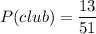
P(club)=(13)/(51)

Using these probabilities, the probability of drawing a heart and a club in that order is:

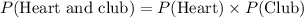
$P(\text{Heart and club})=P(\text{Heart})* P(\text{Club})$

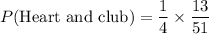
$P(\text{Heart and club})=(1)/(4)* (13)/(51)$

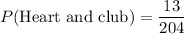
$P(\text{Heart and club})=(13)/(204)$

Therefore, the required probability is
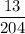(13)/(204) .