Question

) Find the coordinates of the point A' which is the symmetric point

A(3. 2) with respect to the line 2.x + y - 12 = 0.​

Answer 1

Let, coordinate of point A' is (x,y).

Since, A' is the symmetric point A(3, 2) with respect to the line 2x + y - 12 = 0.​

So, slope of line containing A and A' will be perpendicular to the line 2x + y - 12 = 0 and also their center lies in the line too.

Now, their center is given by :

`C( (x+3)/(2), (y+2)/(2))`

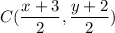
Also, product of slope will be -1 .( Since, they are parallel )

`(y-2)/(x-3) * -2 = -1\\\\2y - 4 = x - 3\\\\2y - x = 1`

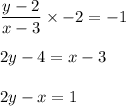
x = 2y - 1

So,
`C( (2y -1 +3)/(2), (y+2)/(2))\\\\C( (2y + 2)/(2), (y+2)/(2))`

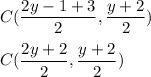
Also, C satisfy given line :

`2* ( (2y + 2)/(2)) + (y+2)/(2) = 12\\\\4y + 4 + y + 2 = 24\\\\5y = 18\\\\y = (18)/(5)`

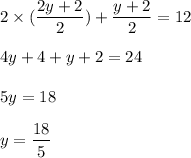
Also,

`x = 2* (18)/(5 ) - 1\\\\x = (31)/(5)`

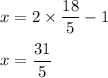
Therefore, the symmetric points is
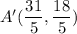`A'((31)/(5), (18)/(5))` .