Question

Solve using the quadratic formula. Show all work. Write each solution in simplest form. No decimals.

Answer 1

Option B

Explanation:

Given quadratic equation is,

12a² + 9a + 7 = 0

By comparing this equation with standard quadratic equation,

hx² + kx + c = 0

h = 12, k = 9 and c = 7

By using quadratic formula,

a =
`(-k\pm√(k^2-4hc))/(2h)`

=
`(-9\pm√(9^2-4(12)(7)))/(2(12))`

=
`(-9\pm√(81-336))/(2(12))`

=
`(-9\pm√(-255))/(24)`

=
`(-9\pm i√(255))/(24)`

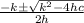
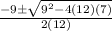
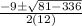
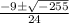
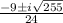
a =
`(-9+ i√(255))/(24),(-9- i√(255))/(24)`

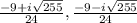
Therefore, Option B will be the correct option.