Question

Since 1995 the cost of a bag of groceries has increased about 2.5% each year. The equation C = 25(1.025)x will give the value of the bag of groceries after any number of years. Predict when the bag of groceries will double in price.

Answer 1

Answer: 28 years

Explanation:

Given

The equation showing the value of the bag after x years is
`C=25(1.025)^x`

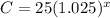
If the price of the bag increased by 2.5%, from the equation, we can deduce that

Initial cost of the bag is 25

Double of the initial value is 50

Insert it in the equation

`\Rightarrow 50=25(1.025)^x\\\Rightarrow 2=1.025^x\\\text{Taking natural log}\\\Rightarrow \ln 2=x\ln (1.025)\\\\\Rightarrow x=(\ln 2)/(\ln 1.025)\\\\\Rightarrow x=28.07\approx 28`

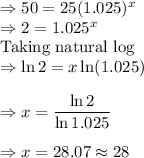
It will take 28 years