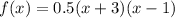Answer:
Explanation:
GIVEN :-
A quadratic function is represented by the graph in which :-
- Vertex of the parabola = (-1 , -2)
- The function intersects x-axis at (-3 , 0) and (1 , 0)
- Y-intercept of the function = -1.5
TO FIND :-
GENERAL CONCEPT USED IN THIS QUESTION :-
A quadratic function has 2 forms :-
- General form → f(x) = ax² + bx + c
- Standard form → f(x) = a(x - h)² + k [∵ where h = x-coordinate of the vertex of the function & k = y-coordinate of the vertex of the function.]
SOLUTION :-
The quadratic function in the graph intersects x-axis at two points (-3 , 0) & (1 , 0). But there are infinite parabolas which also intersect the same two points. And those parabolas have their unique quadratic function.
Method 1 (System of equations method) -
To find the unique quadratic function , you need to use three points on the
curve so that you can form 3 equations & solve them.
Using the General form of quadratic function , substitute the known values for x & y.
Let the three points be -
- (-3 , 0)
- (1 , 0)
- (0 , -1.5)
Substitute (-3 , 0) in general form of function -
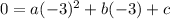
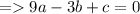 (eqn.1)
(eqn.1)
Substitute (1 , 0) in general form of function -
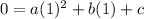
 (eqn.2)
(eqn.2)
Substitute (0 , -1.5) in general form of function -
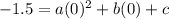
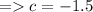
Substitute c = -1.5 in -
1) eqn.1 →

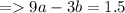
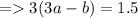
 (eqn.4)
(eqn.4)
2) eqn.2 →
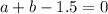
 (eqn.5)
(eqn.5)
Add eqn.4 & eqn.5 to get the value of 'a'.
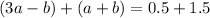
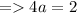
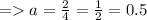
Substitute a = 0.5 in eqn.5 -

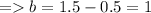
Now, rewrite the function in general form by putting the values of 'a' , 'b' & 'c'.
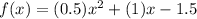
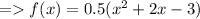
Factorise the quadratic polynomial.
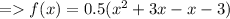
![=> f(x) = 0.5[x(x+3)-1(x+3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/qwyao03amveagmf57weazba4h4bhup7nsl.png)
∴
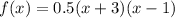
Method 2 (Vertex method) -
Another way to find the function is by taking any point on the curve & using the vertex of the parabola ; substitute the known values for x , y , h & k in the Standard form of the function.
Let that point on the curve be (-3 , 0)
Vertex = (-1 , -2)
Substitute the values of x , y , h & k in Standard form of function.
![0 = a[-3 - (-1)]^2 + (-2)](https://img.qammunity.org/2022/formulas/mathematics/high-school/6npycq6wwypdklywtaytkd7uf8lgoc0bgd.png)
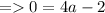
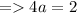

Now rewrite the Standard form of the function by putting the values of h , k & a.
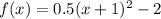
Expand it.
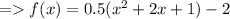

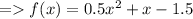
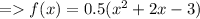
Factorising it will give the final answer.
∴