Answer:
Option 1
Explanation:
Given expression representing the partial sum of the geometric series,
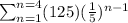
Expression that represents the sum of a geometric series is,
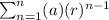
Here, n = number of terms
a = first term
r = common ratio
By comparing both the expressions,
n = 4
a = 125
r =
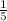
From the given options,
Option 1
First term 'a' = 125
Common ratio 'r' =
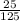 =
=
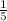
Number of terms 'n' = 4
Therefore, Option 1 will be the correct option.