Question

Find mRT. Assume that segments that appear to be tangent are tangent.

Answer 1

m(arc RT) = 148°

Explanation:

From the picture attached,

Segment RT is a chord and segment RS is a tangent of a circle O meeting at R.

By the property of tangent chord angle,

"Angle formed by an intersecting tangent and chord measures half of the intercepted minor arc"

m(∠SRT) =
`(1)/(2)(\text{minor arc RT})`

`74^0=(1)/(2)m(RT)`

`m(\text{arc RT)}=2(74^0)`

`=148^0`

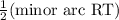
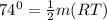
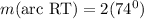
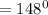
Therefore, measure of minor arc RT is 148°.