Given:
Initial number of bacteria = 3000
With a growth constant (k) of 2.8 per hour.
To find:
The number of hours it will take to be 15,000 bacteria.
Solution:
Let P(t) be the number of bacteria after t number of hours.
The exponential growth model (continuously) is:
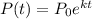
Where,
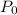 is the initial value, k is the growth constant and t is the number of years.
is the initial value, k is the growth constant and t is the number of years.
Putting
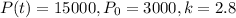 in the above formula, we get
in the above formula, we get


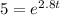
Taking ln on both sides, we get
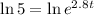
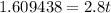
![[\because \ln e^x=x]](https://img.qammunity.org/2022/formulas/mathematics/high-school/m24tge2dslw94bp9jx3y240611r7x9yr3r.png)
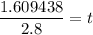
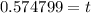
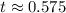
Therefore, the number of bacteria will be 15,000 after 0.575 hours.