Question

I cant solve this problem, and our teacher said that this would be in the test we'll have tomorrow, can someone help me?

A body of m = 6.8kg is launched with a speed of 7.5 m / s towards the top of an inclined plane of 15 ° with respect to the horizontal. in the absence of friction, what displacement does it make before reversing the direction of motion?

Answer 1

d = 11.1 m

Step-by-step explanation:

Since the inclined plane is frictionless, this is just a simple application of the conservation law of energy:

`(1)/(2) m {v}^(2) = mgh`

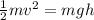
Let d be the displacement along the inclined plane. Note that the height h in terms of d and the angle is as follows:

`\sin(15) = (h)/(d) \\ or \: h = d \sin(15)`

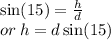
Plugging this into the energy conservation equation and cancelling m, we get

`{v}^(2) = 2gd \sin(15)`

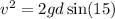
Solving for d,

`d = \frac{ {v}^(2) }{2g \sin(15) } = \frac{ {(7.5 \: (m)/(s)) }^(2) }{2(9.8 \: \frac{m}{ {s}^(2) })(0.259)} \\ = 11.1 \: m`