Question

URGENT

Use technology or a z-score table to answer the question.

The amount spent by customers at a grocery store is normally distributed with a mean of $144.05 and a standard deviation of $34.52.

Approximately what percent of customers at the grocery store spend more than $200?


5.3%

8.2%

91.8%

94.7%

Answer 1

5.3%

Explanation:

The first step is to find the z score corresponding to $200.

`z=(x-\mu)/(\sigma)\\\\z=(200-144.05)/(34.52)\approx 1.62`

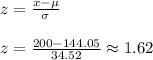
The next step is to find the area under the standard normal curve to the right of z = 1.62. Some graphing calculators can do this, and there are tables that will help, although many of those show areas to the left of a particular z-score.

Calculator (TI-83/84)

See the attached image.

The command uses 1 x 10^99 as "positive infinity" and calculates the area under the normal curve from 1.62 all the way to the right.

Table

See attached table. This table shows areas to the left of a certain z-score.

Find the entry for 1.62 (it's on page 2 highlighted with a red box). The table says the area to the left of 1.62 is 0.9474.

But the area under the entire curve is 1!

This important fact means that the area to the right of z = 1.62 is 1 - 0.9474 = 0.0536, about 5.3%

(To get the area to the right of z, subtract the area to the left of z from 1.)