Question

Eginning at 15,000 feet, a commercial jetliner begins climbing at a rate (in feet per minute) given by f(t)=e0.4t+8 f ( t ) = e 0.4 t + 8 with 0≤t≤20 0 ≤ t ≤ 20 where t t is the time in minutes since the aircraft began climbing. Use the Net Change Theorem to determine the aircraft's elevation after climbing for 15 15 minutes. Round the answer to the nearest foot.

Answer 1

16,126 ft

Explanation:

Using the net change theorem and letting s(t) represent the aircraft's position, and s(0) be the aircraft's position at time t = 0, s(0) = 15000 ft and s(15 be the aircraft's position at time, t = 15 minutes respectively, then,

s(15) - s(0) = ∫₀¹⁵f(t)dt

s(15) - s(0) = ∫₀¹⁵[
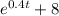`e^(0.4t) + 8`]dt

s(15) - 15000 = [
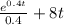`(e^(0.4t))/(0.4) + 8t`]₀¹⁵

s(15) - 15,000 ft =
`(e^(0.4X15))/(0.4) + 8X15 - (e^(0.4 X 0))/(0.4) + 8(0)\\(e^(6))/(0.4) + 120 - (e^(0))/(0.4) + 0\\(403.43)/(0.4) + 120 - (1)/(0.4) + 0\\1008.57 + 120 - 2.5\\1126.07`

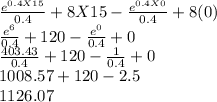
s(15) = 15,000 ft + 1126.07 ft

s(15) = 16,126.07 ft

s(15) ≅ 16,126 ft to the nearest foot