Question

Pls help!!! Pls help!!! Pls help!!!

Answer 1

As
`x \to 2^-`,
`f'(x)=1`.

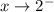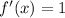Explanation:

See the attached image for the graph of f .

As
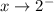`x\to 2^-`, the important part of the definition of f is the first part, valid for [0, 2). On the interval [1, 2), [x] = 1, so
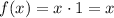`f(x)=x\cdot 1=x`, and the slope is 1.

Interestingly, on the interval [2, 3),
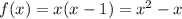`f(x)=x(x-1)=x^2-x`, making
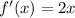`f'(x)=2x`. As
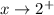`x \to 2^+`, the value of f ' approaches 4. That accounts for the sudden change in direction at the point (2, 2) where the two pieces of the graph connect.

So although the pieces meet at (2, 2) -- f is continuous -- f does not have a (two-sided) derivative at that point because the left-hand derivative and right-hand derivative have different values. There's a "bend" in the graph.