Question

The polynomials ax³ -3 x² +4 and 2x³ -5x+a, when divided by (x-2), leave the remainders p and q are respectively. If p -2 q=4, find the value of a.​

Answer 1

Given:

The polynomial are:

`ax^3-3x^2+4`

`2x^3-5x+a`

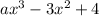
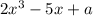
If the above polynomial divided by (x-2) then they leave remainder p and q respectively.

`p-2q=4`

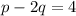
To find:

The value of a.

Solution:

According to the remainder theorem, if a polynomial f(x) is divided by (x-c), then the remainder is f(c).

If the polynomial
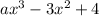`ax^3-3x^2+4` is divided by (x-2), then the remainder is p. So.

`a(2)^3-3(2)^2+4=p`

`8a-12+4=p`

`8a-8=p`

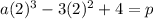
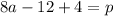
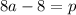
If the polynomial
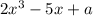`2x^3-5x+a` is divided by (x-2), then the remainder is q. So.

`2(2)^3-5(2)+a=q`

`16-10+a=q`

`6+a=q`

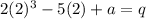
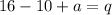
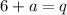
It is given that,

`p-2q=4`

`(8a-8)-2(6+a)=4`

`8a-8-12-2a=4`

`6a-20=4`

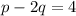
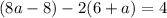
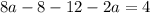
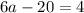
Add 20 on both sides.

`6a=4+20`

`6a=24`

`a=(24)/(6)`

`a=4`

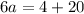
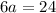
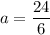
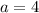
Therefore, the value of a is 4.