Given:
The quadratic equation is:
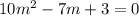
To find:
The solutions for the given equation by using the quadratic formula.
Solution:
If a quadratic equation is
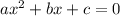 , then the quadratic formula is:
, then the quadratic formula is:
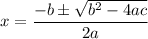
We have,
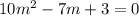
Here,
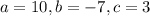 . Using the quadratic formula, we get
. Using the quadratic formula, we get
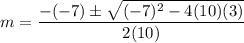
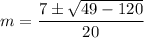
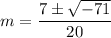
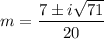
![[\because √(-a)=i√(a),a>0]](https://img.qammunity.org/2022/formulas/mathematics/high-school/q9uovspfqr8o1dyycy4wzbh8vuial01h6g.png)
Therefore, the solution set of the given equation is
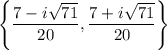 . Hence, the correct option is D.
. Hence, the correct option is D.