Given:
The given quadratic polynomial is :
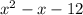
To find:
The quadratic polynomial whose zeroes are negatives of the zeroes of the given polynomial.
Solution:
We have,
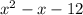
Equate the polynomial with 0 to find the zeroes.
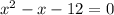
Splitting the middle term, we get
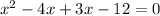
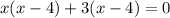
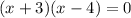
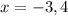
The zeroes of the given polynomial are -3 and 4.
The zeroes of a quadratic polynomial are negatives of the zeroes of the given polynomial. So, the zeroes of the required polynomial are 3 and -4.
A quadratic polynomial is defined as:
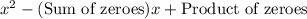

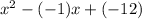
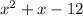
Therefore, the required polynomial is
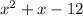 .
.