Answer:
The formula is
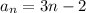
The 14th term is 40, in other words,
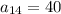
========================================================
Step-by-step explanation:
The given sequence is 1, 4, 7, 10, ...
Subtract each adjacent term:
This shows that each term is increasing by 3. This is the common difference, so d = 3.
The first term is
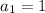
The nth term of the arithmetic sequence is...
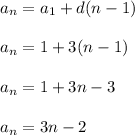
As a check, let's plug in say n = 3 to find that:
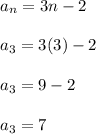
The third term is 7, which matches with the sequence given to us. I'll let you confirm the other values.
-----------
We'll repeat this idea but now for n = 14 to find the 14th term of the sequence.
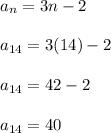
The 14th term is 40.
You can make a table of values to help confirm the answer. In the first column you'll have the values of n (1,2,3,...) all the way up to 14. The second column will consist of the sequence 1, 4, 7, 10, ... each time going up by 3 until you reach the 14th term of 40.