Question

Given the function g(x) = x2 – 10x + 19, determine the average rate of change of

the function over the interval 3 < x < 6.

Answer 1

The average rate of change for g(x) on the interval 3 ≤ x ≤ 6 is -1.

Explanation:

We want to find the average rate of change of the function:

`g(x)=x^2-10x+19`

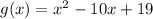
Over the interval:

`3\leq x\leq 6`

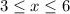
The average rate of change is essentially the average slope of the function. So, we want to find the slope between g(3) and g(6).

Evaluate both points:

`g(3)=(3)^2-10(3)+19=-2`

`g(6)=(6)^2-10(6)+19=-5`

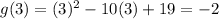
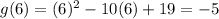
Thus, we obtain the two points (3, -2) and (6, -5).

The slope between them is:

`\displaystyle m=((-5)-(-2))/((6)-(3))=(-3)/(3)=-1`

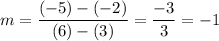
Therefore, the average rate of change for g(x) on the interval 3 ≤ x ≤ 6 is -1.