Answer: Choice C. 27 cm^2
==========================================================
Step-by-step explanation:
It's not directly stated, but I'm assuming that there's symmetry going on in terms of the triangle on the left being a mirror copy of the triangle on the right. If that assumption is true, then we have another "3 cm" along the bottom edge. In total, the bottom edge is 3+6+3 = 12 cm long.
The top edge, parallel to the bottom one, is 6 cm. We'll denote the two parallel sides to be the base lengths and we could write
 . The small subscript just helps us differentiate between the two base lengths.
. The small subscript just helps us differentiate between the two base lengths.
The height is the vertical dashed line of 3 cm. This means h = 3. The height is always perpendicular to the base.
We'll plug those three variables into the area of a trapezoid formula below
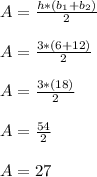
The area is 27 square cm
-----------------------------------
Another way to get the answer is to break the trapezoid into three pieces: two triangles and a rectangle in between.
One triangle has an area of base*height/2 = 3*3/2 = 9/2 = 4.5 square cm, which means two triangles combine to an area of 2*4.5 = 9 square cm.
The rectangle has area of length*width = 6*3 = 18 cm^2
The trapezoid's area is the combination of what we found: 9+18 = 27 cm^2