Given:
The graph of a quadratic function passes through the points (5,31) (3,11) (0,11).
To find:
The equation of the quadratic function.
Solution:
A quadratic function is defined as:
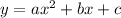 ...(i)
...(i)
It is passes through the point (0,11). So, substitute
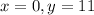 in (i).
in (i).
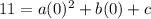
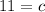
Putting
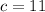 in (i), we get
in (i), we get
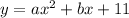 ...(ii)
...(ii)
The quadratic function passes through the point (5,31). So, substitute
 in (ii).
in (ii).
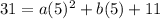
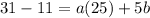

Divide both sides by 5.
 ...(iii)
...(iii)
The quadratic function passes through the point (3,11). So, substitute
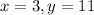 in (ii).
in (ii).
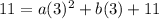
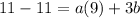
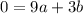
Divide both sides by 3.
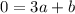 ...(iv)
...(iv)
Subtracting (iv) from (iii), we get
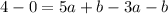
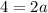
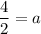
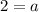
Putting
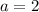 in (iv), we get
in (iv), we get
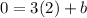
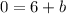

Putting
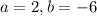 in (ii), we get
in (ii), we get
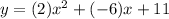

Therefore, the required quadratic equation is
 .
.