Question

Describe the congruence transformation that maps ΔABC onto ΔA′B′C′ in the given figure.

Question 2 options:

A)

Reflection along x-axis; Translation: (x, y) → (x, y – 3)

B)

Reflection along y-axis; Translation: (x, y) → (x, y – 3)

C)

Reflection along y-axis; Translation: (x, y) → (x, y + 3)

D)

Reflection along x-axis; Translation: (x, y) → (x, y)

Answer 1

Answer: Choice B

Reflection along y axis

Translation:
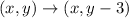`(x,y) \to (x,y-3)` which means we shift 3 units down

===========================================================

Step-by-step explanation:

Let's track point A to see how it could move to point A'.

If we were to reflect point A over the vertical y axis, then A(-4,4) would move to (4,4). The x coordinate flips in sign, but the y coordinate stays the same.

The diagram shows that A' is located at (4,1) instead of (4,4). So a y-axis reflection isn't enough to move A to A', but we can shift that reflected point three units down. That will move (4,4) to (4,1) which is exactly where we want to end up. Note how we subtract 3 from the y coordinate and x stays the same. So that explains the notation
`(x,y) \to (x,y-3)`

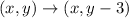
Overall, this points to choice B as the final answer. If we apply these steps to points B and C, you should find that they'll land on B' and C' respectively. Apply this to all of the points on the triangle ABC, and it will move everything to triangle A'B'C'.