Question

The domain of f(x)=ln(x) is negative infinity, infinity.

False, because a logarithmic function is defunded only for positive real numbers

False, because a logarithmic function is defined only for non-negative real numbers

False, because a logarithmic function is defined only for negative real numbers

Answer 1

negative infinity

positive infinity

Step-by-step explanation:

edg 2022

Answer 2

Answer: Choice A

False, because a logarithmic function is defined only for positive real numbers.

===========================================================

Step-by-step explanation:

Using your calculator, you should see that ln(0) is undefined or it leads to some kind of error. The same happens when you try ln(-1) or any other negative number. So ln(x) only allows x > 0. This applies to any log function, and not just the natural log function.

This is why choice A is the answer. Choice B is close, but the use of "non-negative" is not correct because that means 0 is involved. But as explained above, 0 is not allowed as part of the domain.

-----------------

Extra info (optional section)

As for why 0 and negative numbers are not allowed, you have to look carefully at what logs are designed for. They were formed to help solve exponential equations. Consider the following equation

2^x = 16

We could do guess and check to see which value would replace x. You should find that x = 4 is the solution. Though another way to solve is to use logs. The given equation converts to the log form of
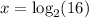`x = \log_2(16)`; note how the number inside the parenthesis is positive. We can't have 2^x equal to a negative value, due to powers of a positive number being a positive result. So that's why we rule out negative numbers as part of the domain. Zero is excluded for similar reasoning.