Question

Which set of side lengths forms a right triangle?

Answer 1

11 inches, 60 inches, 61 inches

Explanation:

This is a right triangle, so the Pythagorean Theorem applies.

The Pythagorean Theorem states that the legs of the triangle, 'a' and 'b'—squared—must equal the hypotenuse, squared.

**Hypotenuse: the longest side of a triangle.**

`a^(2) + b^(2) = c^2`

This sounds a bit complicated, so allow me to explain this to you.

11 and 60: legs of the triangle.

61: hypotenuse

If I were to plug in the numbers into the formula, it would look like this:

`11^2 + 60^2 = 61^2`

This is the same as:

`11 * 11 + 60 * 60 = 61 * 61`

`121 + 3600 = 3721`

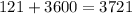
If the legs of the triangle, 121 and 3600, have a sum of the hypotenuse, 3721, then these side lengths can form a right triangle.

The other answer choices, however, do not follow the Pythagorean Theorem.

Answer 2

11-60-61

Explanation:

For right triangle, leg^2+Another leg^2=hypotenuse^2

11^2+60^2=61^2