Answer:
The area of the rectangle ABCD is
 square units.
square units.
Explanation:
From statement we have that rectangle ABCD is formed by the following points:
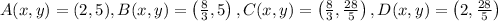 . First, we calculate the length of each side by the Pythagorean Theorem:
. First, we calculate the length of each side by the Pythagorean Theorem:
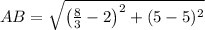

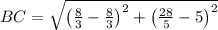
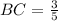
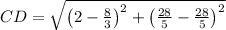
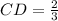
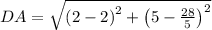
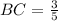
Which satisfies all minimum characteristics for a rectangle. The area of the rectangle ABCD is the product of its base and its height, that is:
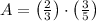
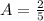
The area of the rectangle ABCD is
 square units.
square units.