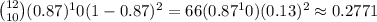Question

John's free throw shooting percentage is 87%. If John shoots 12 free throws in the course of a game, what is the probability he makes exactly 10?

Answer 1

0.2771

Explanation:

This is a binomial probability question. "Makes" is what some writers call a "success." In the binomial probability distribution, the probability of r successes in n trials is

`\binom{n}{r}p^r(1-p)^(n-r)`

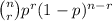
p is the probability of "success."
`\binom{n}{r}=(n!)/(r!(n-r)!)`

In this problem, n = 12, r = 10, p = 0.87 (the 87%).

The probability of exactly 10 made shots out of 12 attempted is

`\binom{12}{10}(0.87)^10(1-0.87)^2 =66(0.87^10)(0.13)^2 \approx 0.2771`