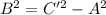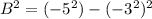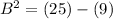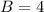Question

The equation of the hyperbola that has a center at ( 6 , 9 ) , a focus at ( 11 , 9 ) , and a vertex at ( 9 , 9 ) (x−C)^2/A^2−(y−D)^2/B^2=1

Answer 1

`A=-3`

`C=6`

`B=4`

`D=9`

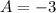
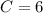
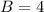
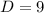
Explanation:

From the question we are told that:

Center of hyperbola at ( 6 , 9 )

Focus of hyperbola at ( 11 , 9 )

Vertex of hyperbola at ( 9 , 9)

Equation of hyperbola
`((x-C)^2)/(A^2) -((y-D)^2)/(B^2)=1`

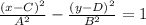
Generally the C and D of the hyperbola equation is mathematically given by

`Centers (6,9)`

`C=6`

`D=9`

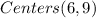
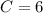
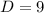
Generally the A and B a of the hyperbola equation is mathematically given by

`A=x_c-x_v`

`A=6-9`

`A=-3`

`C'=x_c-x_f`

`C'=6-11`

`C'=-5`

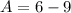
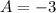
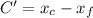
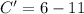
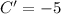
Therefore with Center,Focus ,Vertex on the same line

`B^2=C'^2-A^2`

`B^2=(-5^2)-(-3^2)^2`

`B^2=(25)-(9)`

`B^2=16`

`B=4`