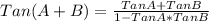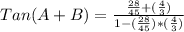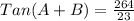Question

If sin ⁡ A = 28 53 sinA= 53 28 ​ and cos ⁡ B = 3 5 cosB= 5 3 ​ and angles A and B are in Quadrant I, find the value of tan ⁡ ( A + B ) tan(A+B).

Answer 1

`Tan(A+B)=(264)/(23)`

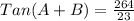
Explanation:

From the question we are told that:

`SinA=(28)/(53)`

`CosB=(3)/(5)`

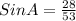
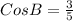
Let X be the adjective side to A

Let Y be the opposite side to B

Generally the equation for X is mathematically given by

`X^2=√(53^2-28^2)`

`X=45`

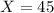
Therefore
`TanA`

`TanA=(28)/(45)`

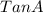
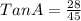
Generally the equation for Y is mathematically given by

`Y^2=√(5^2-3^2)`

`Y=4`

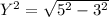
Therefore
`TanB`

`TanB=(4)/(3)`

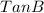
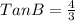
Generally the equation for
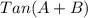`Tan(A+B)` is mathematically given by

`Tan(A+B)=(TanA+TanB)/(1-TanA*TanB)`

`Tan(A+B)=((28)/(45)+((4)/(3)))/(1-((28)/(45))*((4)/(3)))`

`Tan(A+B)=(264)/(23)`