Answer:
La cantidad de días para mantener una población de cerdos mayor en 40 % es de 10 días.
Explanation:
Para una misma cantidad de alimentos, el tiempo de duración de los alimentos (
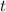 ) es inversamente proporcional a la cantidad de cerdos (
) es inversamente proporcional a la cantidad de cerdos (
 ), es decir:
), es decir:
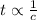
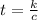 (1)
(1)
Donde
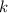 es la constante de proporcionalidad, en días.
es la constante de proporcionalidad, en días.
Podemos eliminar esa constante mediante la siguiente relación:
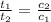 (2)
(2)
Si sabemos que
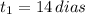 ,
,
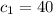 and
and
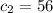 , entonces la cantidad de días asociada una población de cerdos mayor en 40 % es:
, entonces la cantidad de días asociada una población de cerdos mayor en 40 % es:
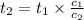
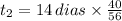
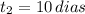
La cantidad de días para mantener una población de cerdos mayor en 40 % es de 10 días.