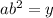Answer:
One
Explanation:
General form of an exponential function:

where a is the initial value, b is the growth/decay factor, and x is the independent variable
If b > 1 the function will grow (increase). If 0 < b < 1 then the function will decay (decrease)
The value Kaylee found is not the constant ratio of successive values. She should use ordered pairs with x-values that differ by 1
This is how Kaylee computed the value of b, which was incorrect as the solution of 8 is for
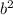 :
:
at (1, 6):
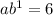
at (3, 48)
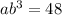

(b is positive since the function is increasing)
However, if Kaylee used the ordered pairs with a difference of one, e.g. x = 1 and x = 2, then she would have computed the correct value of b:
at (1, 6):
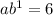
at x = 2: