Given:
The variable cost per unit is $3, fixed costs are $2.
The revenue function is:

where q is the number of thousands of units of output produced.
To find:
The break - even points for company X.
Solution:
The variable cost per unit is $3, fixed costs are $2.
So, the cost function is:
Total cost = Fixed cost + Variable cost × Quantity
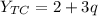
The revenue function is:

At break - even points the profit is zero. It means the cost and revenue are equal.
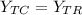

Squaring both sides, we get
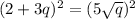

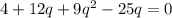

Splitting the middle term, we get
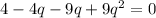
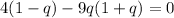
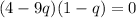
Using zero product property, we get
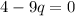 and
and
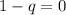
 and
and
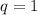
 and
and
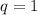
Therefore, the break even points are 0.444 and 1.