Given:
Total number of food cans = 12
Cans of Beets = 8
Cans of corn = 3
Can of beans = 1
To find:
How many distinct orders can the cans be arranged if two cans of the same food are considered identical.
Solution:
To find the distinct ways arrangement, we have a formula:
 ...(i)
...(i)
Where, n is the number of objects and
 are repeated objects.
are repeated objects.
Total number of food cans is 12. So,
 .
.
She has 8 cans of beets. So,
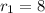
She has 3 cans of corns. So,
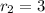
She has 1 can of beans. So,
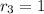
Substituting these values in (i), we get
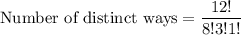
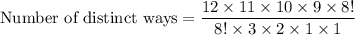
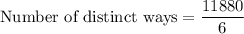
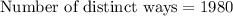
Therefore, the number of distinct orders to arrange the cans is 1980.