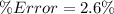Answer:
Step-by-step explanation:
Given
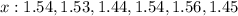
Required
Determine the percentage error
First, we calculate the mean
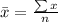
This gives:
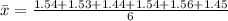
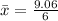
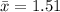
Next, calculate the mean absolute error (E)
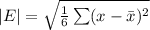
This gives:
![|E| = \sqrt{(1)/(6)*[(1.54 - 1.51)^2 +(1.53- 1.51)^2 +.... +(1.45- 1.51)^2]}](https://img.qammunity.org/2022/formulas/physics/college/5nun6kfbuaeneoas6q7h14xlzlfrim0lsr.png)
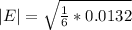
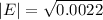
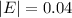
Next, calculate the relative error (R)
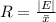
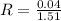
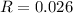
Lastly, the percentage error is calculated as: