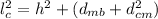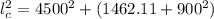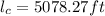Answer:
Step-by-step explanation:
From the question we are told that:
Angle of inclination
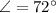
Height
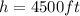
Distance b\w cable base and mountain base
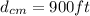
Generally the equation for length of mountain base
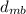 is mathematically given by
is mathematically given by
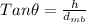
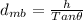
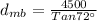
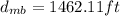
Generally the Pythagoras equation for length of the cable
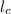 is mathematically given by
is mathematically given by