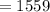Question

The water works commission needs to know the mean household usage of water by the residents of a small town in gallons per day. They would like the estimate to have a maximum error of 0.1 gallons. A previous study found that for an average family the variance is 5.76 gallons and the mean is 19.5 gallons per day. If they are using a 90% level of confidence, how large of a sample is required to estimate the mean usage of water? Round your answer up to the next integer.

Answer 1

The right solution is "1559".

Explanation:

The given values are:

Variance,

`\sigma=√(5.76)`

`=2.40`

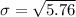
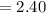
Maximum error,

`M.E=0.1`

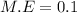
At 90% confidence level,

`\alpha=0.1`

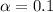
According to the z-table, the critical value will be:

`Zc=1.645`

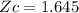
Now,

The sample size will be:

⇒
`n=(Zc* (\sigma)/(E) )^2`

On substituting the values, we get

⇒
`=(1.645* (2.4)/(0.1) )^2`

⇒
`=(1.645* 24)^2`

⇒
`=(39.48)^2`

⇒
`=1558.67`

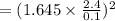
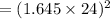
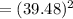
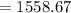
or,

⇒
`=1559`