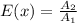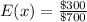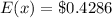Question

Let's compare two different raffles to see which ticket you should buy? A. Raffle 1: 800 raffle tickets are sold $2.00 each. There is one gran prize for $450 and two consolation prizes of $100 each that will be awarded. What is the expected value of one ticket? B. Raffle 2: 350 raffle tickets are sold for $2.00 each. There is one grand prize of $150 and three consolation prizes of $50 each. What is the expected value of one ticket?

Answer 1

(a) The expected value is: $0.40625

(b) The expected value is: $0.4286

Explanation:

Solving (a): Raffle 1

Given

`Tickets=800`

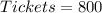
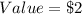`Value = \$2` per ticket

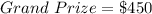`Grand\ Prize = \$450` ---- for 1

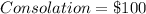`Consolation = \$100` --- for 2

Required

The expected value of each ticket

First, calculate the total amount of the 800 tickets

`Amount = Tickets * Value`

`A_1 = 800 * \$2`

`A_1 = \$1600`

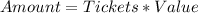
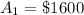
Next, calculate the total amount of the prizes

`Amount = Tickets * Value`

`A_2 = \$450 * 1 +\$100 * 2`

`A_2 = \$450 +\$200`

`A_2 = \$650`

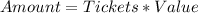
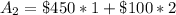
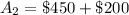
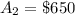
The expected value E(x) of 1 ticket is calculated as:

`E(x) = (A_2)/(A_1)`

`E(x) = (\$650)/(\$1600)`

`E(x) = \$0.40625`

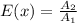
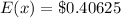
Solving (b): Raffle 2

Given

`Tickets=350`

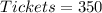
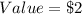`Value = \$2` per ticket

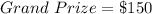`Grand\ Prize = \$150` ---- for 1

`Consolation = \$50` --- for 3

Required

The expected value of each ticket

First, calculate the total amount of the 800 tickets

`Amount = Tickets * Value`

`A_1 = 350 * \$2`

`A_1 = \$700`

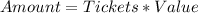
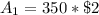
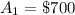
Next, calculate the total amount of the prizes

`Amount = Tickets * Value`

`A_2 = \$150 * 1 +\$50 * 3`

`A_2 = \$150 +\$150`

`A_2 = \$300`

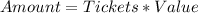
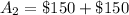
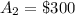
The expected value E(x) of 1 ticket is calculated as:

`E(x) = (A_2)/(A_1)`

`E(x) = (\$300)/(\$700)`

`E(x) = \$0.4286`