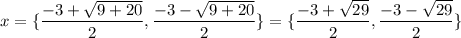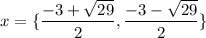Question

Solve using the quadratic formula. Show all work. Write each solution in simplest form. No decimals.

Answer 1

`A) \ \{ (-3 + √(29) )/(2), (-3 - √(29) )/(2) \}`

Explanation:

The quadratic equation to be solved is presented here as follows;

x² + 3·x - 5 = 0

The quadratic formula for a quadratic equation of the form, a·x²+b·x + c = 0, where 'a', 'b', and 'c' are constants and 'x' is unknown, is given as follows;

`x = (-b \pm √(b^2 - 4 \cdot a \cdot c) )/(2 \cdot a)`

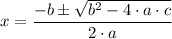
By comparison with the given equation, we have;

a = 1, b = 3, and c = -5

By plugging in the values, we get;

`x = (-3 \pm √(3^2 - 4 * 1 * (-5)) )/(2 * 1)`

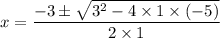
Therefore;

`x = \{(-3 + √(9 + 20) )/(2), (-3 - √(9 + 20) )/(2)\} = \{(-3 + √(29) )/(2), (-3 - √(29) )/(2)\}`

`x= \{(-3 + √(29) )/(2), (-3 - √(29) )/(2)\}`