Question

Complete the square to write each equation in vertex form. Then, state whether the vertex is a minimum or a maximum and give its coordinates.

Answer 1

vertex form: y = (x + 1)² - 3

the vertex is minimum

coordinates of the vertex: (-1, -3)

Explanation:

`y=x^2+2x-2\\\\y=x^2+2x+1-1-2\\\\\bold{y=(x+1)^2-3}`

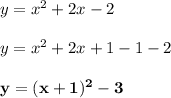
a = 1 > 0 ← it means the parabla opens up, so, the vertex is minimum

The vertex form is y = a(x - h)² + k, where (h, k) is the vertex

So, from y = (x + 1)² - 3 the vertex is: (-1, -3)

Answer 2

• Direction: Opens up
• Coordinates of the vertex: (-1, -3)
• Vertex: -3
• The vertex is a minimum

• Axis of symmetry: x = -1

• Vertex form:
  `y = (x + 1)^(2) -3`